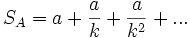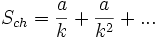Быстроногий Ахиллес никогда не догонит черепаху, если в начале движения черепаха находилась на некотором расстоянии от него.
Действительно, пусть начальное расстояние есть a и пусть Ахиллес всегда бежит в k раз быстрее черепахи. Когда Ахиллес пробежит расстояние a, черепаха отползёт на a/k, когда Ахиллес пройдёт это расстояние, черепаха отползёт на a/k2? и т. д., т. е всякий раз между состязающимися будет оставаться отличное от нуля расстояние.
В этой апории, помимо затруднения отсчитанной бесконечности, имеется и ещё одно. Предположим, что в некоторый момент времени tw Ахиллес догонит черепаху. Запишем путь Ахиллеса
и путь черепахи
Каждому отрезку пути a/kn, пройденному Ахиллесом, соответствует отрезок a/kn+1,пройденный черепахой. Поэтому к моменту встречи Ахиллес должен пройти«столько же» отрезков пути, сколько и черепаха. С другой стороны,каждому отрезку a/kn, пройденному черепахой, можносопоставить равный ему по величине отрезок пути Ахиллеса. Но крометого, Ахиллес должен пробежать ещё один отрезок длины a, то есть он должен пройти на единицу больше отрезков, чем черепаха. Если количество отрезков, пройденное последней, есть α, то получаем
- 1 + α = α
Это последнее затруднение «часть равна целому» явилось впоследствие предметом размышления Галилея, Николая Кузанского и многих других, которые давали этому парадоксу различные интерпретации. Чешский учёный Больцано в первой половине XIX в. установил, что любое бесконечное множествоможет быть приведено во взаимно однозначное соответствие со своейправильной частью. Теперь это свойство иногда применяется в качествеопределения бесконечного множества